< back
Motivation
There has been a long tradition in the epistemology of science of attempting to treat the subject formally using tools from mathematical logic. This began with the general logical approaches of the logical empiricist philosophers of the Vienna Circle and continued in a different direction with the development of the semantic view of theories by Suppes, van Fraassen and others, and continues to this day in more restricted contexts of theories in the foundations of physics.
Many contemporary philosophers of science, however, have foregone a formal approach, preferring more flexible informal views and analyses of science. Along with this shift has been an increasing focus on the role of models in science, often accompanied by a more limited role for theories.
As valuable as both abstract formal and informal approaches can be in elucidating aspects of the epistemology of science, each approach on its own is limited. Formal approaches tend to be very abstract, eliminating from consideration relevant details of how empirical data and experiment affect these formal views of scientific theories. Informal approaches tend to capture nuanced perspectives of the relation between theories, models and the world, but also tend to be limited to a quite restricted area of science and lack a clear way to provide systematic or more general accounts. Moreover, both approaches do not contend with the full complexity of method and content in scientific practice.
Given that scientific method and content has become such an extraordinarily complex phenomenon in its own right, it stands to reason that neither very abstract approaches nor localized informal approaches are well-suited to handling this complexity. I argue that methods developed by scientists for the purposes of studying complex phenomena can be adapted to the task of a scientific study of scientific method and content. This can lead to models of scientific methods and content that are scientifically accurate and deepen our understanding of scientific epistemology.
Epistemological Modeling
I show, in the context of applying scientific theories, that a modeling strategy can be employed in epistemology of science to construct models of aspects of the processes of scientific practice by abstracting models from the details of actual scientific practice. This yields models that are known to be correct in the context they are abstracted from and provides clear epistemological hypotheses outside of this context that can be tested and the models extended.
To illustrate what is involved in this modeling process let us consider a conceptually simple case, that of the construction of a mathematical model of a double pendulum. This is just like a simple pendulum except that there are two weights connected together rather than just one. This is an interesting phenomenon because though it is a very simple mechanical system it exhibits quite complex behaviour, including dynamical chaos.
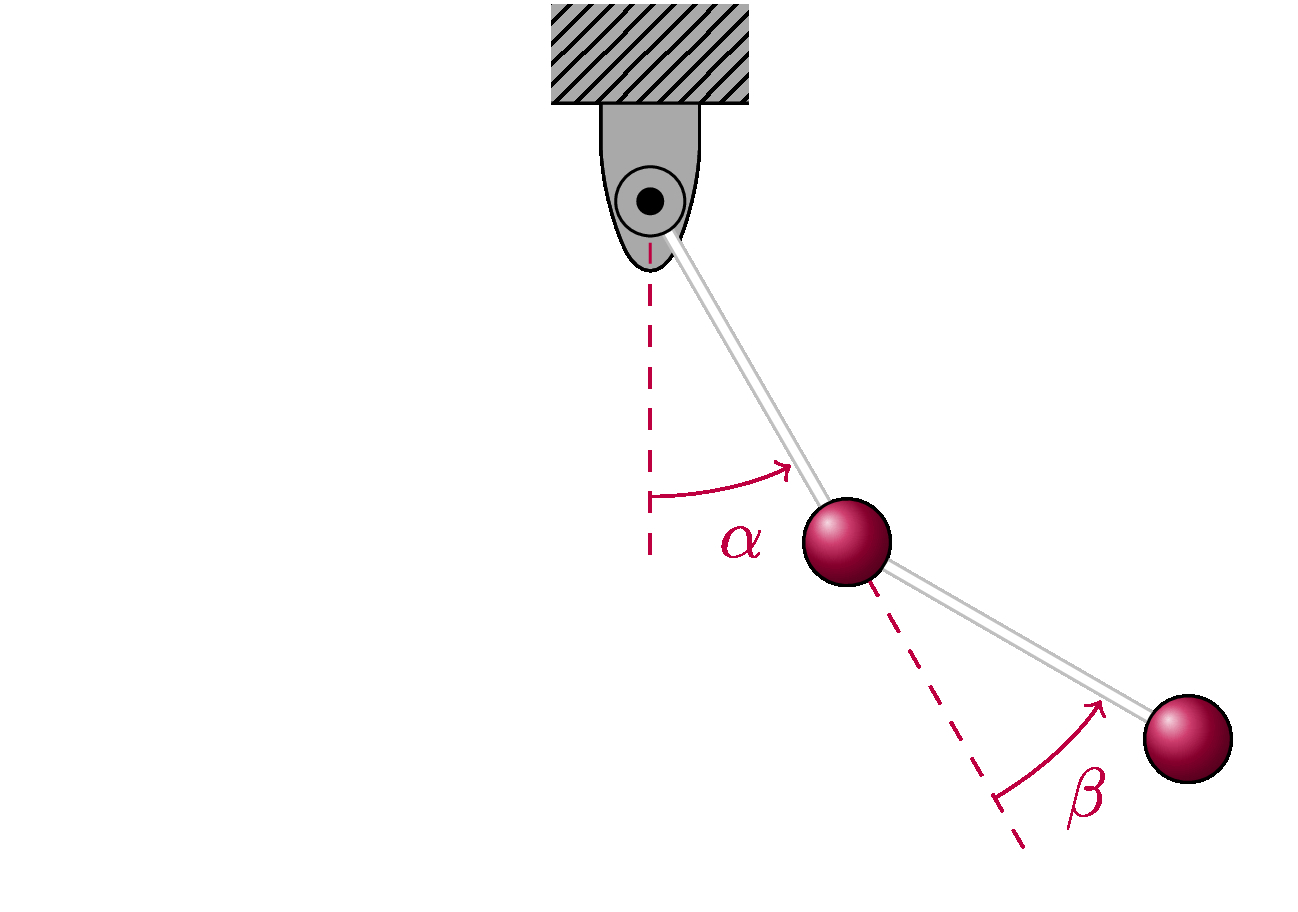
Now, since we are doing epistemological modeling, the phenomenon we are concerned with is not the physical pendulum itself, but rather the inferential process used to understand and predict its behaviour. Thus, we aim to construct a model of the process by which we take knowledge of the structure and behaviour of the physical system, basic equations of physics and mathematical methods and use them to construct a model from which we can learn about the physical system.
Epistemological Phenomenology
(word to the wise: understanding the epistemological points does not require grasping the equations)
Before we can construct an epistemological model, then, we need to understand how the process actually works in practice. Thus, we must study the epistemological phenomena and extract, or abstract, from that some sort of model.
In this simple case of the double pendulum, the epistemological process begins with two main things: 1) prior experience with pendulums, which tells us what information we can usefully ignore, e.g., the mass of rods if the weights are heavy enough; and 2) basic equations and methods of relevant physical theories, e.g., Hamiltonian mechanics, which provide starting points and methods for model construction.
Assuming that we have made the strongest reasonable simplifying assumptions based on our knowledge of pendulums, we may then use Hamiltonian mechanics to construct a mathematical model. We have simplified the model so that motion can be described using four parameters, these are the two angles \(\alpha\) and \(\beta\) (shown in the figure above) and the corresponding angular momenta $l_{\alpha}$ and $l_{\beta}$. When we formulate the appropriate model, the result looks like the following,
\begin{equation}\label{hameqns} \dot{\bf q}=\frac{\partial H}{\partial{\bf p}},\quad \dot{\bf p}=-\frac{\partial H}{\partial{\bf q}}, \tag{1}\end{equation}
\[ \scriptsize H({\bf q},{\bf p}) = -2\cos\alpha-\cos(\alpha+\beta)+\frac{l_{\alpha}^2-2(1+\cos\beta)l_{\alpha}l_{\beta}+(3+2\cos\beta)l_{\beta}^2}{3-\cos2\beta}, \]
where ${\bf q}=(\alpha,\beta)$ is a vector quantity fixing the position of the double pendulum and ${\bf p}=(l_{\alpha},l_{\beta})$ is a vector quantity fixing the momentum. This is our mathematical model of the double pendulum.
With the model constructed, the task is then to determine how to find out how ${\bf q}$ and ${\bf p}$ change over time, i.e., to determine the behaviour of the model, in different circumstances. The trouble is that we do not have an analytical method to solve these equations. At this point, then, we must use numerical methods, which means converting the continuous-time dynamics above to a discrete-time dynamics that has behaviour as close as possible to the original model---but it also solvable.
Hamiltonian systems have the property that their energy is strictly conserved over time. Thus, ideally we would have a numerical method that would share this energy conservation property. It turns out it is possible to do this using so-called symplectic methods, which guarantee that energy is (very nearly) conserved over very long time periods.
One such method, suitable for Hamiltonian problems, is the Störmer-Verlet method. Applying this method, the equations above are converted into the discrete-time dynamics characterized by the equations
\begin{equation}\label{stovereqns} {\bf q}_{n+1}={\bf q}_n+\frac{h}{2}({\bf k}_1+{\bf k}_2),\quad {\bf p}_{n+1}={\bf p}_n-\frac{h}{2}({\bf m}_1+{\bf m}_2), \tag{2}\end{equation}
\[ \scriptsize {\bf k}_1=\frac{\partial H}{\partial{\bf p}}({\bf q}_n,{\bf p}_n+\frac{h}{2}{\bf m}_1),\ {\bf k}_2=\frac{\partial H}{\partial{\bf p}}({\bf q}_n+\frac{h}{2}({\bf k}_1+{\bf k}_2),\ {\bf p}_n+\frac{h}{2}{\bf m}_1), \]
\[ \scriptsize {\bf m}_1=\frac{\partial H}{\partial{\bf q}}({\bf q}_n,{\bf p}_n+\frac{h}{2}{\bf m}_1),\ {\bf m}_2=\frac{\partial H}{\partial{\bf q}}({\bf q}_n+\frac{h}{2}({\bf k}_1+{\bf k}_2),{\bf p}_n+\frac{h}{2}{\bf m}_1), \]
where the continuous ${\bf q}$ and ${\bf p}$ from equation \eqref{hameqns} have been replaced by the discrete position ${\bf q_n}$ and momentum ${\bf p_n}$ values at particular times $t_n=t_0+nh$.
We have now replaced the continuous equations with simpler discrete ones, but we actually cannot solve these equations analytically either! We can, however, transform them into executable code in a fairly direct way, which we could not do with the original continuous-time dynamics. Thus, to continue our inferential process, we must discretize further, and write code so that a computer can find approximate solutions to the numerical method. This is an implementation of the numerical method.
An example of such an implementation in Matlab or Octave code is the following function $\texttt{stover}$ that computes solutions to Hamilton's equations using the Störmer-Verlet method.
[Note: for those following the equations, that the f and g appearing in this code correspond to ${\bf f}$ and ${\bf g}$ in the equations $\dot{\bf q}={\bf f}=\frac{\partial H}{\partial{\bf p}}$ and $\dot{\bf p}=-{\bf g}=-\frac{\partial H}{\partial{\bf q}}$ in equation \eqref{hameqns} and the corresponding partial derivatives in the expressions for ${\bf k}_1$, ${\bf k}_2$, ${\bf m}_1$ and ${\bf m}_2$ from equation \eqref{stovereqns}.]
function [tout,xout] = stover (f, g, Df, Dg, tspan, yi, zi, h, tol, nmax)
# usage: stover (f, g, Df, Dg, tspan, yi, zi, h, tol, nmax)
# f: an anonymous function or function handle to f(t,y,z)
# g: an anonymous function or function handle to g(t,y,z)
# Df: an anonymous function or function handle defining the Jacobian of f
# Dg: an anonymous function or function handle defining the Jacobian of g
# yi: initial condition for variable y
# yi: initial condition for variable x
# tspan: interval defining the time span of the integration
# h: time step
# tol: the convergence tolerance for Newton's methods
# nmax: maximum iterations of Newton's method per time step
t0 = tspan(1);
tfinal = tspan(2);
tdir = sign(tfinal-t0);
h = tdir*abs(h);
t = t0;
y = yi(:);
z = zi(:);
neqn = length(y);
# Initialize output
tout=t;
xout=[y', z'];
while t ~= tfinal
# Stretch the step if t is close to tfinal
if abs(h) >= abs(tfinal - t)
h = tfinal - t;
endif
# Compute a step
# Compute l1, implicit
l1 = h;
for i = 1:neqn-1
l1(end+1,1) = h;
endfor
for j = 1:nmax
Gx = l1 - g(t, y, z+h/2*l1);
DGx = eye(neqn) - h/2*Dg(t, y, h/2*l1);
dl1 = -DGx\Gx;
l1 = l1 + dl1;
if (max(abs(dl1)) < tol)
# dl1
break
end
endfor
# Compute k1
k1 = f(t,y, z + h/2*l1);
# Compute k2, implicit
k2 = h;
for i = 1:neqn-1
k2(end+1,1) = h;
endfor
for j = 1:nmax
Fx = k2 - f(t, y + h/2*(k1 + k2), z+h/2*l1);
DFx = eye(neqn) - h/2*Dg(t, y + h/2*(k1 + k2), h/2*l1);
dk2 = -DFx\Fx;
k2 = k2 + dk2;
if (max(abs(dk2)) < tol)
# dk2
break
end
endfor
# Compute l2
l2 = g(t, y + h/2*(k1 + k2), z+h/2*l1);
# Take a step
y = y + h/2*(k1+k2);
z = z + h/2*(l1+l2);
t = t+h;
# Update output
tout(end+1,1)=t;
xout(end+1,:)=[y', z'];
end
endfunction
If we correctly code the equations for the Hamiltonian dynamics \eqref{hameqns} above, we can then compute solutions to our model of the double pendulum under different conditions. Notice that without writing and running the code, we cannot complete inferences concerning how the model will behave under different conditions. It is only by running an algorithm on a physical computing device that we are able to make model inferences feasible, i.e., actually accessible or possible.
An example of the sort of inferences that become feasible with an implemented solution algorithm is the following simulation, which exhibits chaotic behaviour in the motion of the double pendulum. For this simulation we need specific initial conditions, which we choose to be
\[ \alpha(0)=90^{\circ},\quad \beta(0)=-90^{\circ},\]
which at the initial moment leaves the upper arm held horizontal and the lower arm dangling freely. To display the chaos (generic extreme sensitivity to initial conditions) the two pendulums are started in almost the exact same position at rest (the initial angles $\alpha=-\beta\simeq 90^{\circ}$ differ only by a tenth of a degree) and then dropped. Despite this tiny difference in initial conditions their trajectories rapidly diverge from one another, which becomes increasingly visually evident until it becomes obvious.
At this point we have feasible access to solutions of our mathematical model. Even in this simple case, there is much more to the modeling process, since we then need to test the consequences of the model and then add more complexity to it if and when it fails to agree with observations or experiment. For our purposes here, however, this gives us a sense of the kind of complexity of process involves in the scientific modeling process.
What About the Epistemological Model?
With a simple epistemological process to work with, we can now consider its implications for the construction of an epistemological model. The inferential complexity just for such a conceptually simple example makes it clear that there is no obvious best way to model the inferential process---it depends on what it is we seek to understand about the inferences. The logical tradition in scientific epistemology, however, gives us an excellent place to start.
The logical empiricists modeled the relation between a scientific theory in terms of correspondence rules, which correlated theoretical and observational languages and gave the theory meaning. In term of the semantic view, focus shifted to hierarchies of related models (Suppes) and an understanding of the semantics of theories in terms of state-space models (van Fraasen).
We can see that these approaches capture important features of the inferential process for the double pendulum since: 1) we needed to pass through a number of models to get to one we could actually solve, viz., empirical model of the physical system, theoretical model, numerical model, computer model; and 2) the theoretical model is a state-space model, the state given in position-momentum space. I contend, however, that these approaches are missing something significant from the point of view of formal languages.
The semantic view of theories takes, from a formal point of view, theories or models to all be presented in a uniform logical way, viz., in terms of a semantics of sets and relations. Individual characteristics of particular languages are generally viewed as unimportant, as are the reasons for choosing particular languages within which to formulate models. A good epistemological model of double pendulum inferences should account for these things.
I argue that a natural way to model the inferential process, from a formal language point of view, is to regard the inferential process as a sequence of transformations between languages in the interest of reaching a language where the desired inferences are feasible. Consider how this looks in terms of the four languages we have identified:
- Informal observation language (English): here we can easily describe what we experience and what experiences would correspond to certain theoretical predictions, but we have very limited ability to make predictions or explanations of behaviour. So we move to a...
- Continuous-time dynamical systems model: here we can easily describe an abstract version of the target system and, in principle, predict and explain how it will be have under any circumstances. Supposing that the solutions of the model actually provide a valid model of the target, further inference is blocked because we cannot compute how to evolve the system forward in time. So we move to a...
- Discrete-time dynamical systems model: here we have an algorithmic way to compute new states of the model based on old ones, and in a way that provides results that are extremely close to the states predicted by the continuous model. But further inference is still blocked because we cannot solve the equations to compute time-steps. So we move to a...
- Coded instructions in a high level computer language: here we now have a feasible way to compute approximate new states of the model based on old ones, and in a way that provides results that are extremely close to the states predicted by the continuous model. Thus, this step allows us to feasibly complete the inferential process by re-interpreting the computed states in the continuous model.
An important thing to observe here is that there are three kinds of languages that provide very different kinds of information and play a very different role in the inferential process: 1) natural language, which provides rich descriptive capacity and a context for physical interpretation of mathematical models; 2) mathematical language, which provides powerful conceptual frameworks and an ability to determine exact behaviour under particular constraints or conditions; and 3) computer languages, which provide powerful means for interpreting algorithms and an a means to instruct a machine to efficiently compute solutions.
Another important thing to observe here is that the transformations between these languages have the following special property:
They simultaneously preserve desired information about the structure and behaviour of the target system and make that desired information more feasibly accessible.
It is reasonable to conclude or hypothesize, then, that the languages we use in scientific inference are used because they have this special property in the manner demanded by the epistemic circumstances.
All of this is quite informal, which is fine to a point, but I implied above that scientific epistemology was in need of more than just an informal approach. I also said, however, that formal approaches tend to be overly abstract and miss important details. This produces a need, I claim, for more flexible formal methods.
To address this issue, I provide in my dissertation a "quasi-formal" logical model of the kind of inferential process I have modeled informally here. I argue that this provides an example, however limited, of a scientific approach to epistemological modeling. It functions to elucidate in a more precise manner the insight contained in the "special property" identified above. This leads to a picture of feasible scientific as a recursive process of transformations between languages or conceptual frameworks terminating in a framework where inference is fully feasible so that conclusions can be back-interpreted into other frameworks in the sequence.
In the context of a scientific epistemology of science, this represents a hypothesis concerning the structure of real scientific inference. A topic of future work is to test the validity of this hypothesis by examining scientific inference in quite different contexts, and to use these tests to develop, refine and extend the model and modeling approach.
